
“Sztuczna inteligencja (AI) może mieć wpływ na wycenę nieruchomości na kilka sposobów. Oto kilka przykładów:
- Przetwarzanie dużych ilości danych: AI może szybko przetwarzać duże ilości danych dotyczących nieruchomości, takich jak ceny sprzedaży w okolicy, cechy nieruchomości i inne czynniki, które mogą mieć wpływ na cenę. Dzięki temu możliwe jest szybsze i bardziej dokładne wycenianie nieruchomości.
- Predykcja cen: AI może również wykorzystywać modele predykcyjne do przewidywania przyszłych cen nieruchomości. Może to pomóc w określeniu, czy dana nieruchomość będzie rosnąć w wartości w przyszłości i w jaki sposób.
- Oszczędność czasu i kosztów: AI może również pomóc w oszczędzeniu czasu i kosztów związanych z wyceną nieruchomości. Dzięki automatyzacji pewnych procesów możliwe jest szybsze przetwarzanie danych i uzyskanie wyników.
- Ocena stanu nieruchomości: AI może również być wykorzystywana do oceny stanu nieruchomości, co może pomóc w określeniu jej wartości. Na przykład, poprzez analizę zdjęć nieruchomości możliwe jest określenie, czy wymaga ona remontu lub napraw, co może mieć wpływ na jej cenę.
Ogólnie rzecz biorąc, AI może mieć pozytywny wpływ na wycenę nieruchomości poprzez umożliwienie szybszego i bardziej dokładnego przetwarzania danych oraz poprzez ułatwienie oszacowania przyszłych cen i stanu nieruchomości.”*
*tekst powyższy wygenerowano przez chatGPT (https://openai.com/blog/chatgpt/) na zapytanie: “napisz o wpływie sztucznej inteligencji na wycenę nieruchomości”, czyli faktycznie jest to wypowiedź AI o samej sobie 🙂
…wróćmy jednak do tematu.
Do zbudowania przykładowej sieci neuronowej użyjemy języka Python oraz biblioteki TensorFlow, która pozwala na zdefiniowanie sieci neuronowej. Użyjemy także innych bibliotek języka python, takich jak pandas, numpy, sklearn oraz matplotlib.
Na początku zbudujemy model którego użyjemy do predykcji wartości funkcji y=sin(x).
Tworzymy zbiór wartości x i y dla funkcji y=sin(x) w przedziale x od 0 do 10.
import pandas as pd
import numpy as np
dane_list=[]
for nr in range(1,100,1):
x=nr/10
y=np.sin(x)
new_row=(x,y)
dane_list.append(new_row)
dane_pd=pd.DataFrame(dane_list, columns=['x','y'])
Dzielimy nasz zbiór na część przeznaczoną do wyuczenia sieci (zbiór treningowy) oraz na część przeznaczoną na przetestowanie sieci (zbiór testowy):
from sklearn.model_selection import train_test_split
import tensorflow as tf
train_set, test_set = train_test_split(dane_pd, test_size=0.2, random_state=42)
target=train_set.pop('y')
dane_pd_train=train_set[['x']]
tf.convert_to_tensor(dane_pd_train)
Podstawową jednostką sieci neuronowej jest perceptron, który jest odpowiednikiem neuronu. Perceptrony ułożone są w warstwy: wejściowe, ukryte i wyjściowe. Załóżmy, że nasz model składał się będzie z warstwy wejściowej, 3 warstw ukrytych (po 100, 200 i 100 neuronów) oraz warstwy wyjściowej.
Definiujemy model sieci neuronowej jaki będziemy chcieli użyć do obliczeń:
model=tf.keras.models.Sequential()
model.add(tf.keras.layers.Input(shape=dane_pd_train.shape[1:]))
model.add(tf.keras.layers.Dense(100,activation="relu"))
model.add(tf.keras.layers.Dense(200,activation="relu"))
model.add(tf.keras.layers.Dense(100,activation="relu"))
model.add(tf.keras.layers.Dense(1))
model.compile(loss="mean_squared_error", optimizer="adam")
Trenujemy model:
history=model.fit(dane_pd_train,target, epochs=100,validation_split = 0.2)
Generujemy wykres (średnia funkcja straty uczenia zmierzone w każdej epoce, zarówno dla zestawu uczącego (loss), jak i dla walidacyjnego (val loss)):
import matplotlib.pyplot as plt
hist = pd.DataFrame(history.history)
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.xlabel('Epoch')
plt.ylabel('Error [MSE]')
plt.legend()
plt.show()
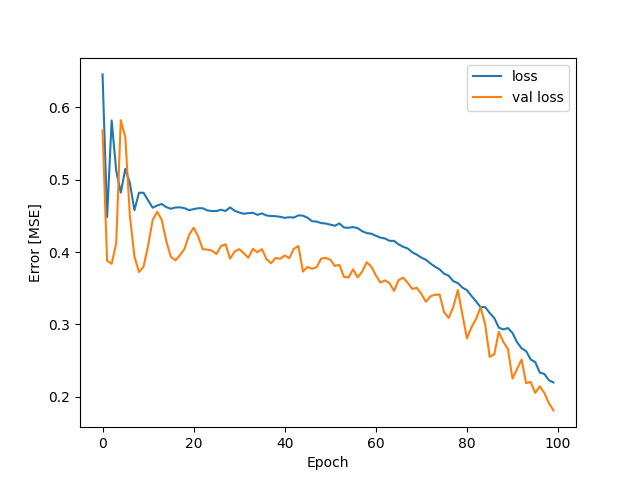
Jak widać z wykresu model jest prawdopodobnie niedotrenowany, zwiększamy liczbę epok w modelu:
history=model.fit(dane_pd_train,target, epochs=400,validation_split = 0.2)
Otrzymujemy wykres:
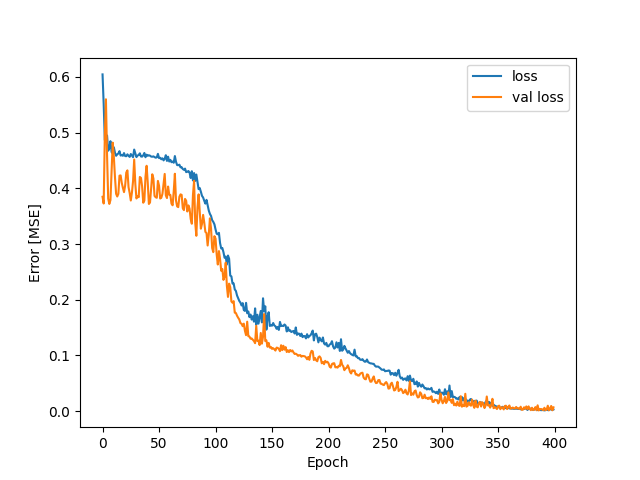
Otrzymaliśmy dość zbieżne linie loss. Sprawdźmy zatem na zbiorze testowym jakość predykcji modelu (do obliczenia predykcji na zadanym zbiorzez testowym służy polecenie model.predict(), pozostała część kodu to przygotowanie danych do wykresu):
target_spr=test_set.pop('y')
tf.convert_to_tensor(test_set)
target_pred=model.predict(test_set)
dane_wynik_testu=pd.DataFrame(columns=['x', 'y','target_pred'])
x=np.array(test_set['x'])
y=np.array(target_spr)
i=0
for elements in target_pred:
row_to_append={'x': x[i],'y': y[i],'target_pred': target_pred[i][0]}
dane_wynik_testu=dane_wynik_testu.append(row_to_append, ignore_index=True)
i+=1
plt.plot(dane_pd['x'],dane_pd['y'],'o',label='dane początkowe')
plt.plot(dane_wynik_testu['x'],dane_wynik_testu['target_pred'],'rX',label='wynik predykcji (uczenia)')
plt.xlabel('x')
plt.ylabel('y, y_predict')
plt.legend()
plt.show()
Otrzymujemy wykres:
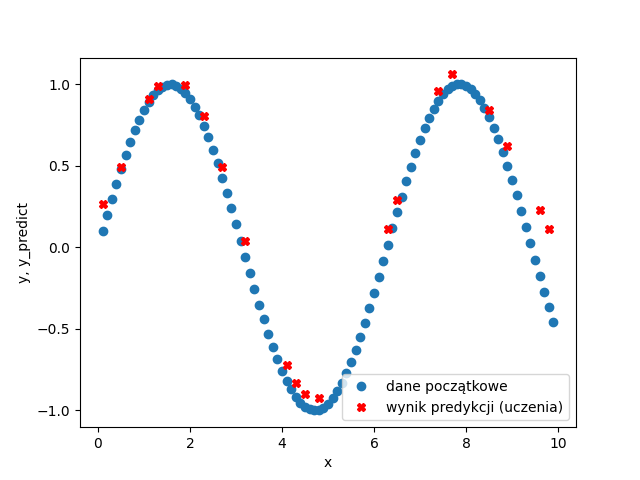
Jak widać nasz model całkiem dobrze przewiduje warości y na podstawie zadanych x znajdujących się w zakresie x-ów które poslużyły do wytrenowania modelu. Oczywiście moglibyśmy zwiększyć dokładność modelu poprzez zwiększenie ilości epok, inne skonfigurowanie sieci, większą ilość neuronów itp, ale dla zadanej funkcji y=sin(x) model wydaje się być zadowalający.
Można oczywiście przeprowadzić trudniejszą predykcję poprzez skomplikowanie funkcji y(x) (np. jako funkcji wielu zmiennych – jedynym ograniczeniem jest dostępna moc obliczeniowa).
Można także zastąpić zmienne np. cechami nieruchomości i wyuczyć model do przewidywania ceny/wartości nieruchomości.
